| Zadania dla klasy III gimnazjum | W ZESPOLE SZKÓŁ W WIDUCHOWEJ |
 |
nie ma drogi specjalnie dla królów |
|||
| Zadania dla klasy III gimnazjum | W ZESPOLE SZKÓŁ W WIDUCHOWEJ |
 |
nie ma drogi specjalnie dla królów |
|||
| Ośmiokąty. | |||||||||||||||||||
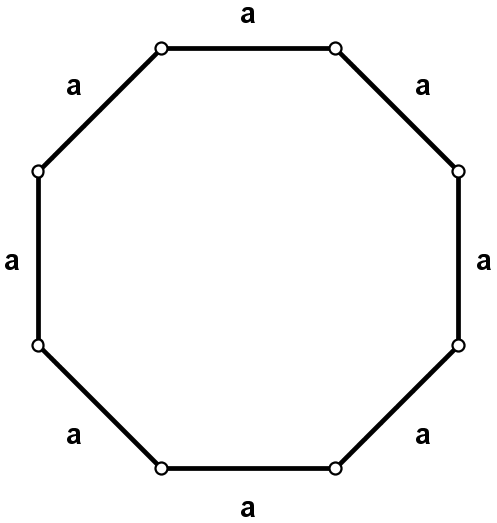
| Opiszę dwa rodzaje ośmiokątów, którymi się zajmę. | |||||||||||||||||||
|
 |
||||||||||||||||||
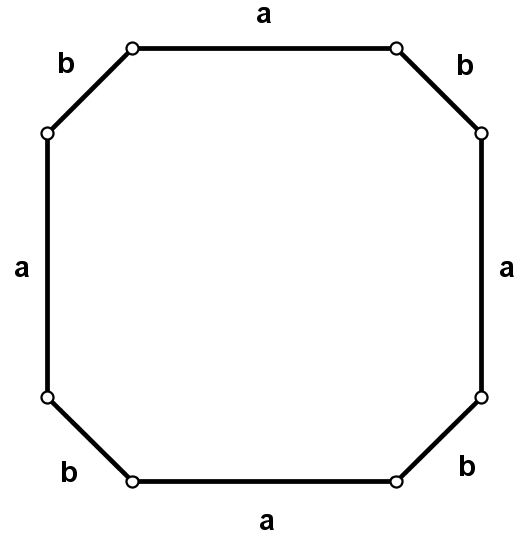
| Ośmiokąty foremne | Ośmiokąty, które mają wszystkie kąty wewnętrzne równe oraz boki równoległe mają równej długości, boki leżące obok siebie są różnej długości. | ||||||||||||||||||
| Oba typy ośmiokątów mają miary kątów wewnętrznych równe 1350. Te ośmiokąty będę nazywał odpowiednio ośmiokątem 1 i ośmiokątem 2. | |||||||||||||||||||
Wiadomo,
że jeżeli trójkąt prostokątny równoramienny ma
przyprostokątne o długościach równych a, a to
przeciwprostokątna ma długość równą
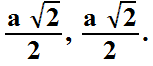 Ta druga informacja pomoże w obliczeniu pola jednego i drugiego
ośmiokąta.
Ta druga informacja pomoże w obliczeniu pola jednego i drugiego
ośmiokąta.
| |||||||||||||||||||
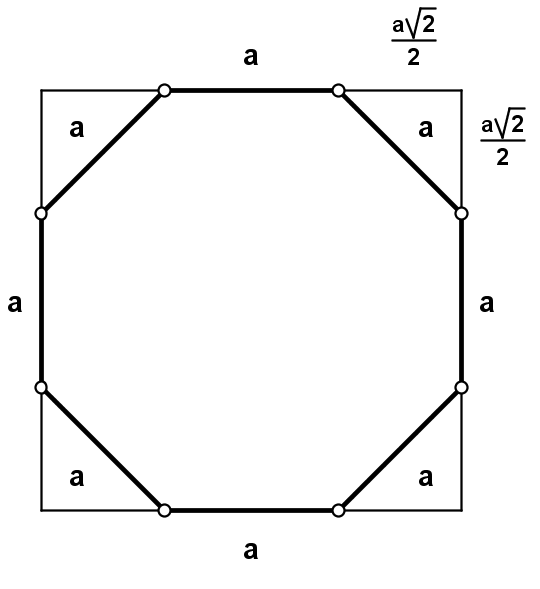
| Dopełniamy ośmiokąty trójkątami prostokątnymi równoramiennymi (rysunki). Powstają kwadraty. | |||||||||||||||||||
 |
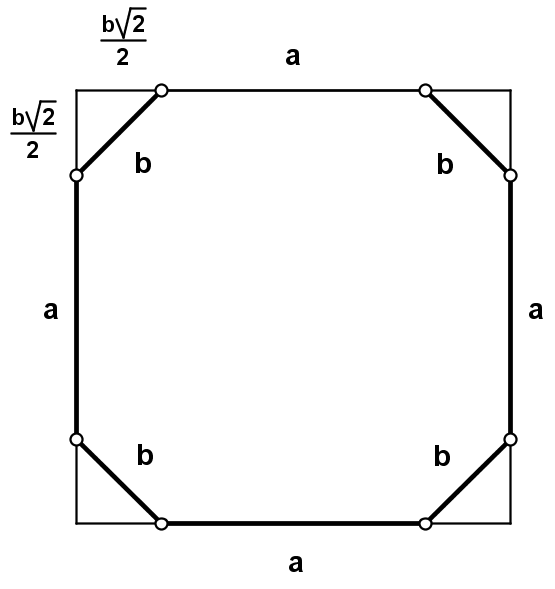 | ||||||||||||||||||
Kwadraty
mają długości boków:
| |||||||||||||||||||
Pola kwadratów wynoszą odpowiednio: | |||||||||||||||||||
| Pole każdego trójkąta równoramiennego prostokątnego w ośmiokącie I i ośmiokącie II wynosi odpowiednio: | |||||||||||||||||||
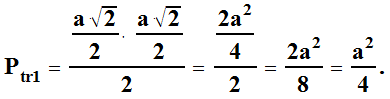 Są
4 takie trójkąty. Są
4 takie trójkąty.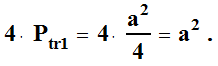 | |||||||||||||||||||
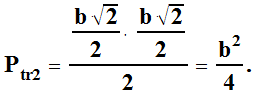 Analogicznie Analogicznie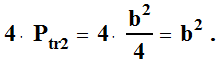 | |||||||||||||||||||
| Pole ośmiokąta 1 to różnica pól kwadratu 1 i 4 pól trójkątów. Analogiczna sytuacja jest w ośmiokącie 2. Stąd: | |||||||||||||||||||
| oraz | |||||||||||||||||||
|
Układając alfabetycznie
| |||||||||||||||||||
 |
 | ||||||||||||||||||
| Opracował: Mariusz Baszak | |||||||||||||||||||
| Powrót do głównej strony | |||||||||||||||||||