twierdzenia Pitagorasa kwadrat |
W ZESPOLE SZKÓŁ W WIDUCHOWEJ |
 |
nie ma drogi specjalnie dla królów |
|||
twierdzenia Pitagorasa kwadrat |
W ZESPOLE SZKÓŁ W WIDUCHOWEJ |
|
nie ma drogi specjalnie dla królów |
|||
| POWRÓT DO WYBORU DLA KLASY 8 | |||||||||||||||||||
| PODSTAWOWE WZORY DOTYCZĄCE KWADRATU | |||||||||||||||||||
| Uwaga Wprawadzamy następujące oznaczenia: | |||||||||||||||||||
|
a - bok kwadratu, d - długość przekątnej kwadratu. | |||||||||||||||||||
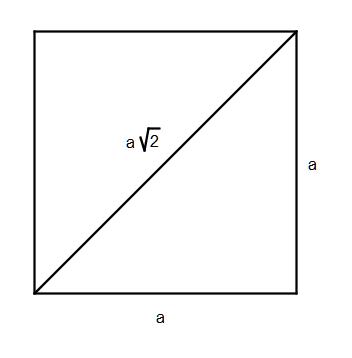 Rys.1 |
Długość przekątnej d w kwadracie jest  razy większa od
długości boku kwadratu a(rys.1) | ||||||||||||||||||
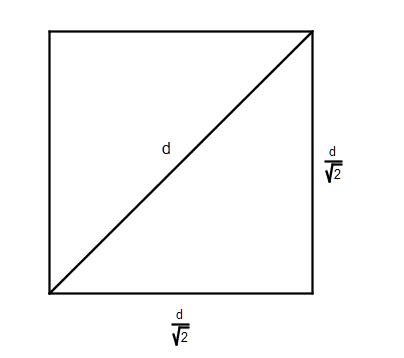 Rys.2 |
Długość boku kwadratu a jest razy mniejsza od
długości przekątnej kwadratu d (rys.2) | ||||||||||||||||||
| Przykłady obliczenia
długości przekątnej kwadratu d
na podstawie długości boku kwadratu a. | |||||||||||||||||||
 | |||||||||||||||||||
| DŁUGOŚĆ BOKU KWADRATU | | | |
DŁUGOŚĆ PRZEKĄTNEJ KWADRATU | |||||||||||||||||
| | | |||||||||||||||||||
 | | |  | |||||||||||||||||
| | | |||||||||||||||||||
 | | |  | |||||||||||||||||
| | | |||||||||||||||||||
 | | |  | |||||||||||||||||
| Przykłady obliczenia
długości boku kwadratu a na podstawie długości przekątnej kwadratu d. | |||||||||||||||||||
 | |||||||||||||||||||
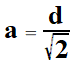| DŁUGOŚĆ PRZEKĄTNEJ KWADRATU | | | | DŁUGOŚĆ BOKU KWADRATU | |||||||||||||||||
| | | |||||||||||||||||||
 | | |  | |||||||||||||||||
| | | |||||||||||||||||||
 | | |  | |||||||||||||||||
| | | |||||||||||||||||||
 | | |  | |||||||||||||||||
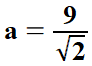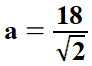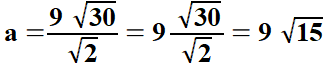| W ostatnim przykładzie jest ułamek, w którym licznik i mianownik jest pierwiastkiem. Kreskę ułamkową zastępujemy dzieleniem, czyli mamy iloraz pierwiastków. Przypominam, że iloraz pierwiastków tego samego stopnia (tu drugiego) jest pierwiastkiem z ilorazu liczb podpierwiastkowych (30 : 2 = 15). | |||||||||||||||||||