Wiadomości dotyczące twierdzenia Pitagorasa dla klasy 8		MATEMATYKA W ZESPOLE SZKÓŁ W WIDUCHOWEJ			W matematyce nie ma drogi specjalnie dla królów	Powrót do głównej strony

POWRÓT DO WYBORU DLA KLASY 8

PODSTAWOWE WIADOMOŚCI DOTYCZĄCE TWIERDZENIA PITAGORASA

Obliczanie przyprostokątnej

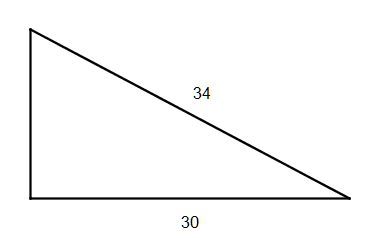
Mamy daną długość przeciwprostokątnej 34 i długość drugiej przyprostokątnej równą 30. Oblicz długość drugiej przyprostokątnej. Tworzymy rysunek pomocniczy (rys. 1).

Rys. 1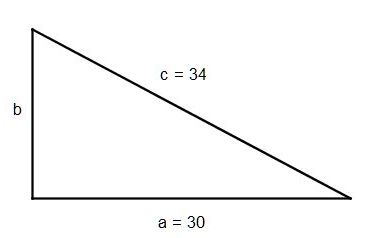

Rys. 2

Na rysunku pomocniczym oznaczamy a = 30, c = 34, nieznany bok jako b (rys.2).

Zapisujemy twierdzenie Pitagorasa:

Podstawiamy wartości.

Obliczamy b2, a następnie b.

Znając podstawowe wartości potęg drugiego stopnia liczb od 2 do 20, znamy również wartości odpowiednich pierwiastków.

Odp.: Długość nieznanej przyprostokątnej wynosi 16.

Uwaga: Wartość 342 musimy obliczyć pisemnie. Tego typu obliczeń nie wolno liczyć w pamięci, ponieważ najczęściej kończy się to błędnymi obliczeniowymi.

Obliczanie przeciwprostokątnej

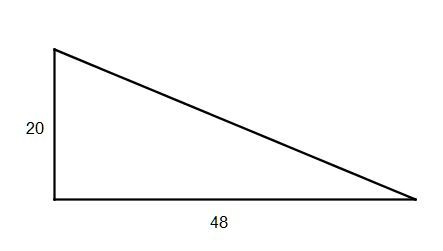
Mamy daną długość jednej przyprostokątnej 20 i długość drugiej przyprostokątnej równą 48. Oblicz długość przeciwprostokątnej. Tworzymy rysunek pomocniczy (rys. 3).

Rys. 3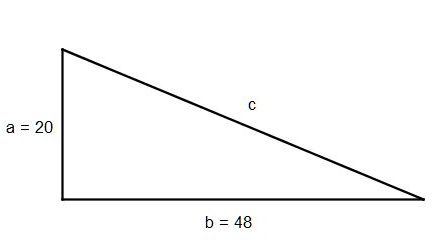

Rys. 4

Na rysunku pomocniczym oznaczamy a = 20, b = 48, nieznany bok jako c (rys.4).

Zapisujemy twierdzenie Pitagorasa:

Podstawiamy wartości.

Obliczamy c2, a następnie c.

Ponieważ liczba nie jest wartością drugiej potęgi żadnej liczby od 2 do 20, dlatego rozkładamy liczbę 2704 na czynniki pierwsze (rozkład 1). Na drugim rozkładzie (rozkład 2) widać pogrupowane zostały powtarzające się liczby. Obok widać dlaczego grupujemy powtarzające się liczby.

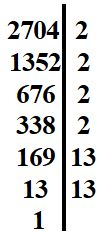Rozkład 1

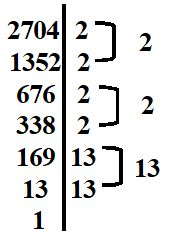Rozkład 2

Odp.: Długość nieznanej przeciwprostokątnej wynosi 52.

Uwaga 1: Wartość 482 musimy obliczyć pisemnie.

Uwaga 2: Liczby, które w rozkładzie na czynniki pierwsze grupujemy w pary, nie muszą występować jedne za drugimi. Wtedy liczby powtarzające się jednakowo podkreślamy.