rok szkolny 2017/2018 |
W ZESPOLE SZKÓŁ W WIDUCHOWEJ |
 |
nie ma drogi specjalnie dla królów |
|||
rok szkolny 2017/2018 |
W ZESPOLE SZKÓŁ W WIDUCHOWEJ |
 |
nie ma drogi specjalnie dla królów |
|||
| POWRÓT DO WYBORU ZADAŃ | |||||||||||||||||||
| Zadania dla klasy III gimnazjum rok szkolny 2017/2018 | |||||||||||||||||||
| Zad.1. Z przystających trapezów równoramiennych AHFG, HBKD, CGEK utworzono figurę, w której powstały dwa trójkąty równoboczne ABC, DEF. Boki tych trójkątów mają długości odpowiednio 10 cm i 4 cm (patrz rysunek). W trapezie HBKD oblicz: | |||||||||||||||||||
| a)
długości ramion |KB| oraz |HD|; b) wysokość |KL|; c) pole tego trapezu. | 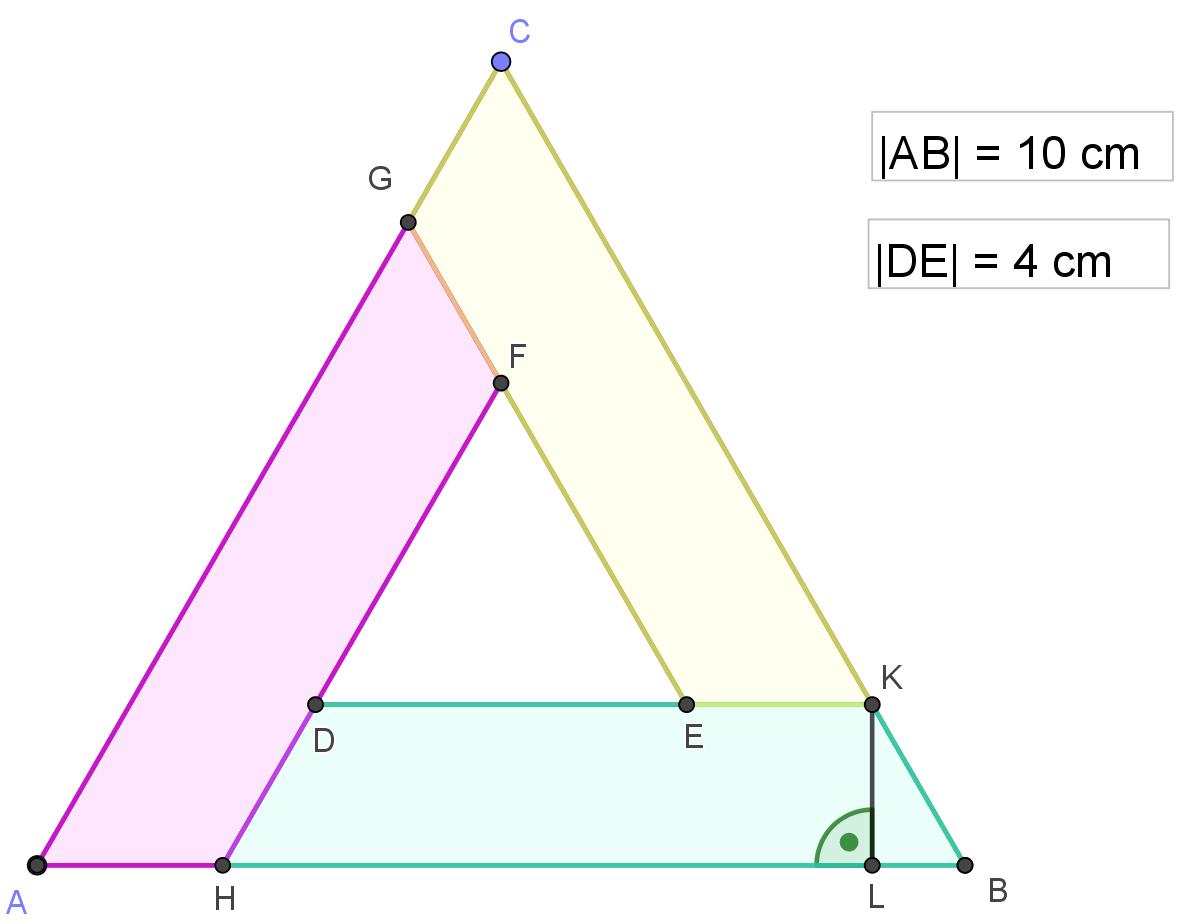 | ||||||||||||||||||
| Zad.2. Na rysunku pokazano dwa przystające kwadraty ABCD i CEFG o boku długości a oraz deltoid CBHE, którego dwa boki są o długości a i dwa boki o długości
3a.
Oblicz pole deltoidu CBHE. Uwaga: Kąt ECB jest kątem prostym. | 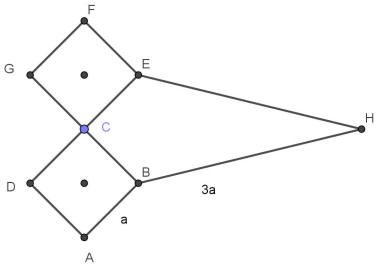 | ||||||||||||||||||
| Zad.3. W grze w bilard gra się bilami wykonanymi z żywicy fenolowej. Na początku gry piętnaście bil ustawia się w specjalnym trójkącie. Zdejmuje się trójkąt i w równo ułożone bile uderza się (dodatkową) bilą rozgrywającą (rys.) Środki na skraju ułożonych bil (rys.) tworzą trójkąt równoboczny. Na rysunku podałem w milimetrach wysokość tego trójkąta. | |||||||||||||||||||
| Oblicz: a) promień kuli bilardowej w cm; b) objętość jednej kuli dla c) objętość wszystkich 16 kul biorących udział w grze (bez podstawiania liczby | 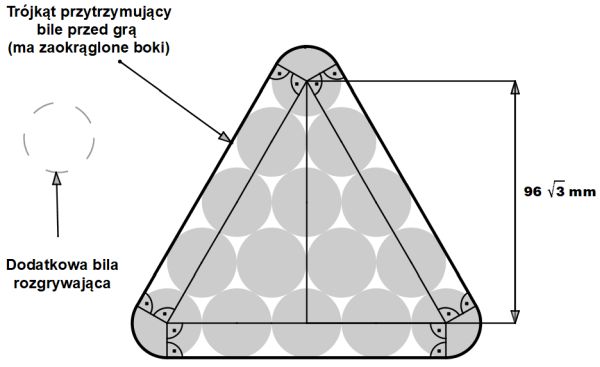 | ||||||||||||||||||