| Pole pięciokąta foremnego | MATEMATYKA W ZESPOLE SZKÓŁ W WIDUCHOWEJ |
 |
W matematyce nie ma drogi specjalnie dla królów |
Powrót do głównej strony | ||
| Pole pięciokąta foremnego | MATEMATYKA W ZESPOLE SZKÓŁ W WIDUCHOWEJ |
 |
W matematyce nie ma drogi specjalnie dla królów |
Powrót do głównej strony | ||
| POWRÓT DO WYBORU CIEKAWOSTEK |
|
||||||||||||||||||
| WSTĘP | |||||||||||||||||||
| Zajmę się pięciokątem foremnym. W klasie 8 uczniowie zapoznają się twierdzeniem Pitagorasa. Przy okazji poznają wzór na pole trójkąta równobocznego oraz pole sześciokąta foremnego. Znają oczywiście wzór na pole czworokąta foremnego, bo oczywiście to
jest wzór na pole kwadratu. Jeden z uczniów zapytał mnie, czy na egzaminie może ktoś od nich wymagać wzór na pole pięciokąta foremnego. Powiedziałem, że nie ma takiej możliwości, ponieważ ten wzór jest bardzo skomplikowany - nawet ja nie jestem w stanie się go nauczyć na pamięć. Ponadto, aby go wyprowadzić trzeba mieć wiadomości wykraczające poza wiedzę byłego ucznia gimnazjum, ale również licealista mógłby mieć kłopoty z jego wyprowadzeniem. Tak jak powiedziałem dla wyprowadzenia tego wzoru będzie nam potrzebna znajomość wiadomości ze szkoły podstawej takich jak: - suma miar kątów w trójkącie, - własności trójkątów przystających, - twierdzenie Pitagorasa, - wzór na miarę kąta wielokąta foremnego, - włączaniem i wyłączaniem liczby pod i spod pierwiastka. Ze szkoły średniej posłużę się tamkimi wiadomościami jak: - własności trójkątów podobnych, - rozwiązanie równania kwadratowego, - wzorami skróconego mnożenia, - funkcjami trygonometrycznymi (dopiero w drugiej części przy wyprowadzania innej postaci tego wzoru). Jeszcze jako ciekawostkę dodam, że na istnienie w pięciokącie foremnym dużej ilości trójkątów podobnych zwrócił nam uwagę mój wspaniały wykładowca algebry na studiach Pan doktor Czesław Wowk. Przechodzę więc do wyprowadzania wzoru. | |||||||||||||||||||
| UWAGA: Podczas wyprowadzania wzoru ciężko cały czas przewijać stronę do rysunków, które są opisywane. Dlatego też w trakcie opisu są dostępne odnośniki do potrzebnych rysunków. Można sobie włączyć odnośnik do rysunku 1 i rysunku 2 lub odnośnik do rysunku 3 i rysunku 4 (oba rysunki są na jednej wspólnej podstronie). | |||||||||||||||||||
 Rys. 1 |
 Rys. 2 |
||||||||||||||||||
|
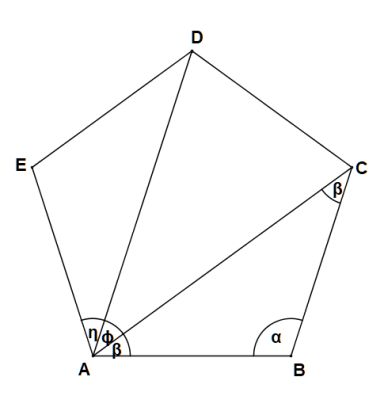
Na początku w pięciokącie rysuję dwie przekątne AC i AD (rys. 1). Widać, że są one równej długości.
Obliczam kąt wewnętrzny 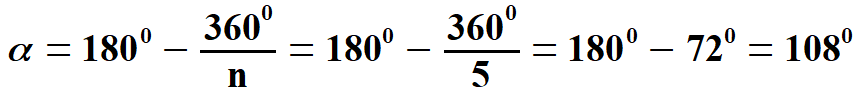
Stąd wiadomo, że zachodzą równości:
Widać, że 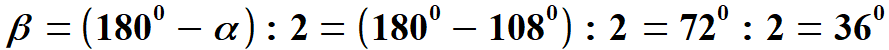
Trójkąty
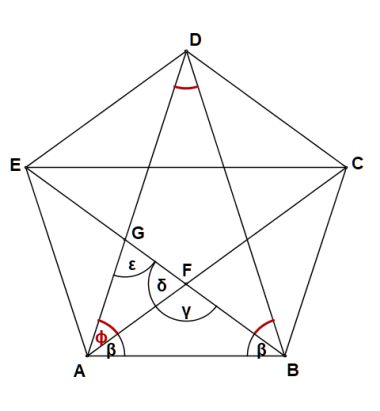
Rysujemy wszystkie przekątne, łatwo obliczyć, że w pięciokącie jest ich tylko pięć (rys. 2). Jak już wcześniej pisałem wszystkie przekątne pięciokąta foremnego są tej samej długości, ponieważ tylko mogą powstać z połączenia co drugiego wierzchołka. Widać, że 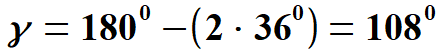
oraz ponieważ kąty Wiemy, że 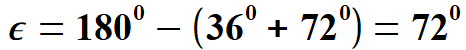
Jest jeszcze trzeci trójkąt podobny do tych trzech, mianowicie Trójkątem równoramiennym jest również Są w nim kąty o miarach 360, 360, 1080. Powyższe fakty pozwolą nam na obliczenia. Tworzymy dwa nowe rysunki: rys. 3 i rys. 4. | |||||||||||||||||||
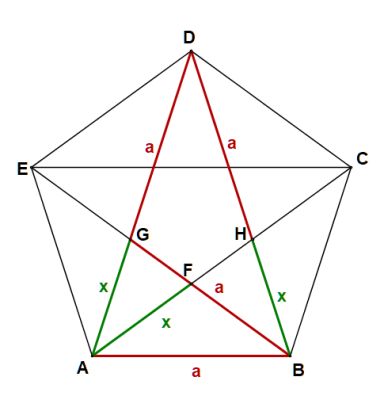 Rys. 3 |
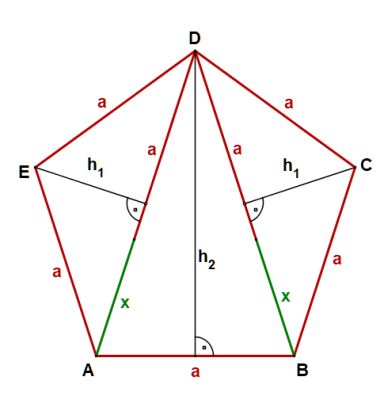 Rys. 4 |
||||||||||||||||||
|
Przeanalizujemy rys. 3.
oraz Wszystkie trzy odcinki oznaczyłem kolorem czerwonym. Zakładamy, że długość a (długość boku pięciokąta froremnego) jest znana. Widać, że długość przekątnej pięciokąta foremnego jest równa sumien x + a. Mając daną wielkość a obliczymy długość x. Z równości odpowiednich kątów wynika podobieństwo dwóch trójkątów równoramiennych, które omówiłem wyżej tj. W W Z podobieństwa trójkątów (tutaj równoramiennych), wiemy, że stosunek długości podstaw będzie równy stosunkowi długości ramion, co oczywiście jest równe skali podobieństwa. Otrzymujemy więc 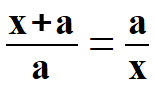 , ,
Uwaga: Mamy tu do czynienia z tzw. złotym podziałem. Jeżeli popatrzymy na przekątną to stosunek długości całej przekątnej x + a do dłuższej części tej przekątnej a jest równy stosunkowi dłuższej części tej przekątnej a do krótszej części przekątnej x. Rozwiązujemy otrzymane równanie. Otrzymaliśmy równanie kwadratowe, gdzie niewiadomą jest x, natomiast a jest daną liczbą. Przypominam trójmian kwadratowy: 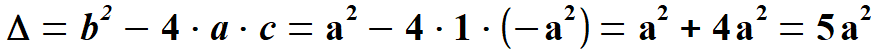
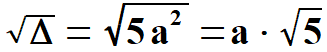 Obliczamy x1 oraz x2. 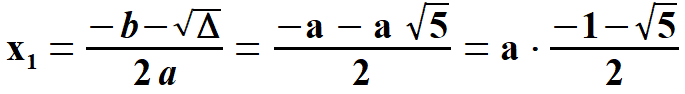 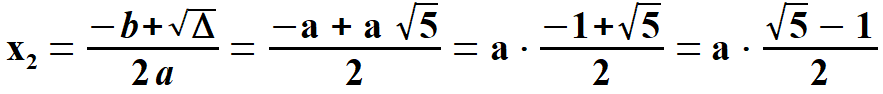
Widać, że x1 < 0, natomiast x2 > 0. Oczywiście wybieramy x2 . Stąd 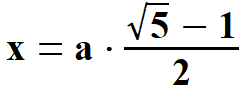 Na rys. 5 widać, że aby obliczyć pole pięciokąta należy obliczyć pola trzech równoramiennych trójkątów, w tym dwóch przystających. Musimy jednak dowiedzieć się jaką długość mają wysokości tych trójkątów h1 oraz h2. Obliczymy to z Twierdzenia Pitagorasa. Podstawą trójkąta 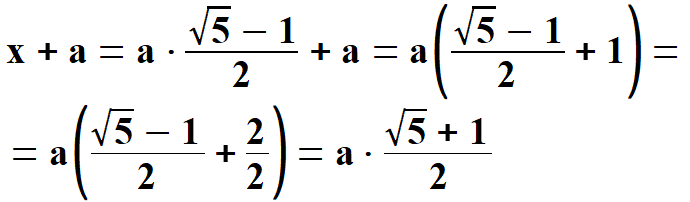 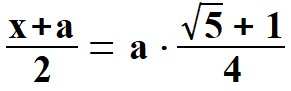 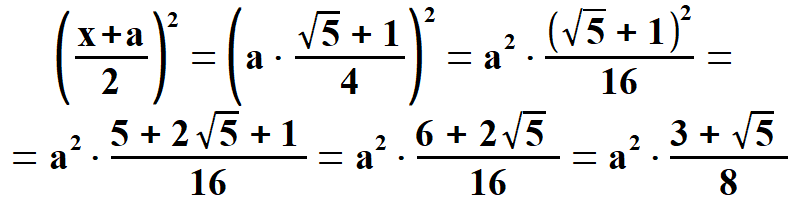 Po drodze wykorzystałem wzory, z których będę jeszcze korzystał. Są to: dodawanie i odejmowanie ułamków o tych samych mianownikach, wyłączanie czynnika przed nawias, kwadrat iloczynu, kwadrat sumy dwóch wyrażeń. Obliczam wysokość h1 z twierdzenia Pitagorasa. 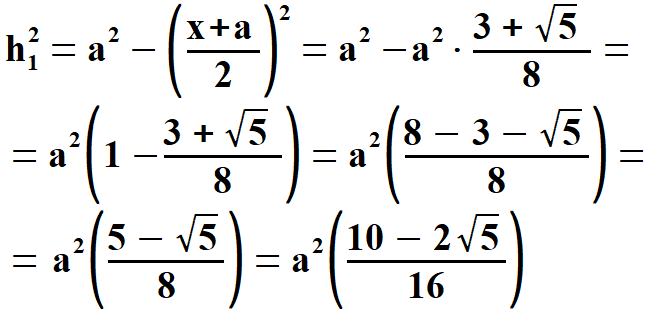 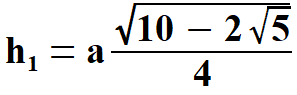 Obliczam pole trójkąta 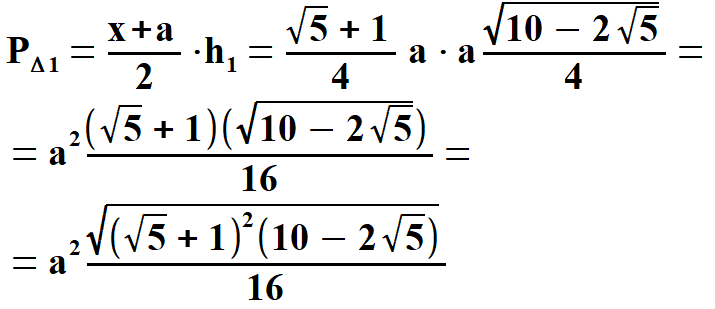 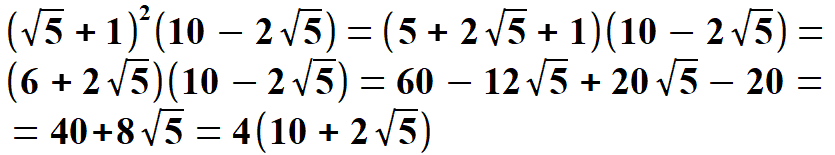 To co wyszło podstawiam z powrotem pod pierwiastek i przekształcam otrzymując pole każdego z w/w trójkątów. 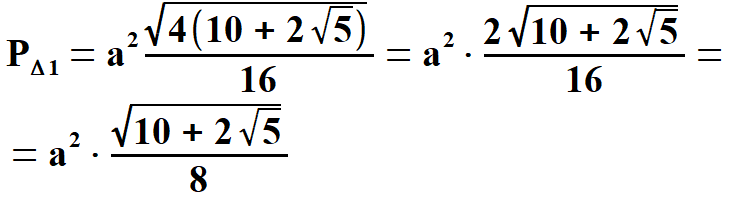 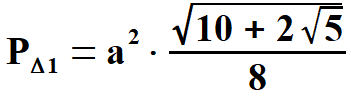 Obliczamy w analogiczny sposób pole trójkąta (już bez komentarza). 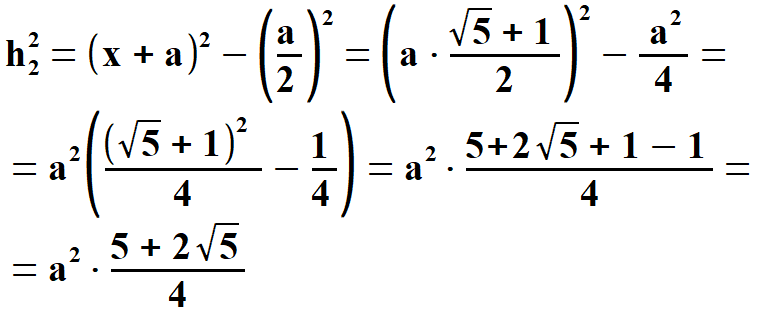 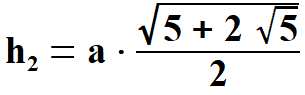 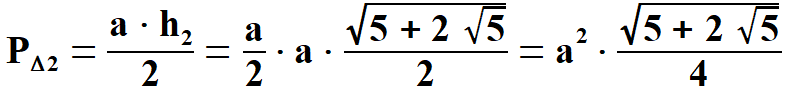
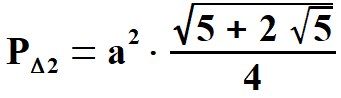 Obliczam 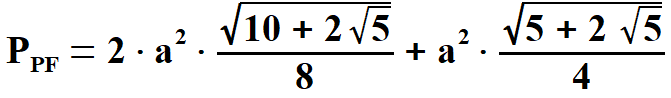 | |||||||||||||||||||
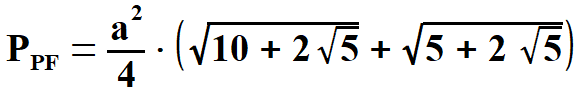 | |||||||||||||||||||
Obliczyłem pole pięciokąta foremnego o boku a.
W dalszej części poprowadzę czytelnika przez funkcje trygonometryczne oraz drugi wzór, który jest w poradnikach matematycznych wynikający z trygonometrycznego wzoru na pole trójkąta (można w ten wzór wejść tutaj lub na początku tej strony). | |||||||||||||||||||
|
| |||||||||||||||||||
| Opracował: Mariusz Baszak | |||||||||||||||||||