Pole pięciokąta foremnego trygonometria

POLE PIĘCIOKĄTA FOREMNEGO
WYNIKAJĄCEGO
ZE WZORU TRYGONOMETRYCZNEGO
NA POLE TRÓJKĄTA

WSTĘP

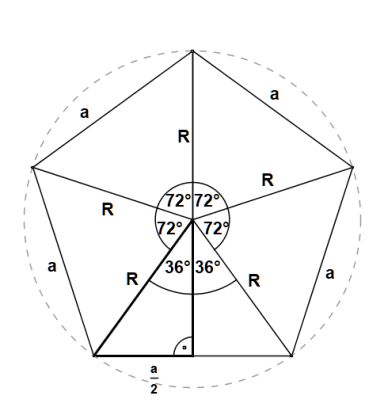
Zajmę się drugim wzorem na pole pięciokąta foremnego, wynikającego ze wzoru trygonometrycznego na pole trójkąta. Podzielę pięciokąt foremny na pięć trójkątów równoramienych, których ramiona są promieniami okręgu opisanego na pięciokącie foremnym (rys. 3). Jest to znana metoda obliczania pól wielokątów foremnych. Ta część jest przeznaczona dla uczniów ciekawych matematyki oraz tych, którzy znają podstawy trygonometrii, czyli wiedzą, jakie są definicje funkcji trygonometrycznych, znają wzór na pole trójkąta, o którym pisałem wyżej i umieją dobrze przekształcać wzory. Nie będę już tyle komentował jak przy wzorze poprzednim.
Przechodzę więc do wyprowadzania wzoru.

UWAGA:
Podczas wyprowadzania wzoru ciężko cały czas przewijać stronę do rysunków oraz wzorów potrzebnych do dalszych obliczeń. Dlatego też w trakcie opisu są dostępne odnośniki do potrzebnych rysunków i wzorów. Można będzie sobie włączyć odnośniki do rysunku 1 i rysunku 2 + wzory

RYS.1 | RYS.2 +wzory
(oba rysunki ze wzorami są na jednej wspólnej podstronie).
Odnośniki są w kilku miejscach tekstu, wystarczy je wywołać tylko jeden raz. Otwiera się podstrona z dwoma rysunkami oraz z wzorami bez zamykaniam strony głównej. W trakcie czytania możemy w każdej chwili przełączyć się między tekstem a potrzebnymi rysunkami i wzorami.
Tekst do rysunku 3 jest dość krótki, więc łatwo już do niego powrócić w trakcie czytania.

WYPROWADZENIE WZORU NA POLE PIĘCIOKĄTA FOREMNEGO ZA POMOCĄ FUNKCJI TRYGONOMETRYCZNYCH

Rys. 1

Rys. 2

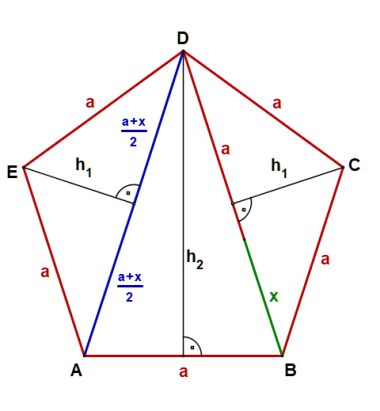
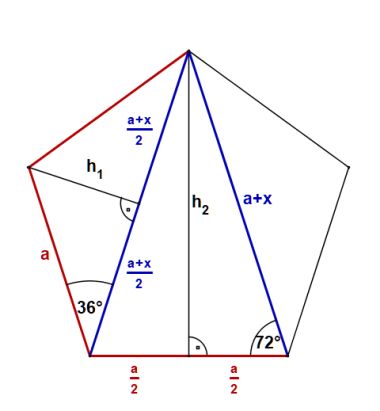
Na początku w pięciokącie rysuję jeszcze raz trójkąty jak przy pierwszym wyprowadzeniu wzoru na pole pięciokąta foremnego.
Przypomne wzory na długości odcinków, które będą nam potrzebne.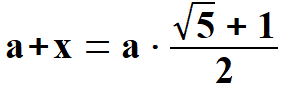

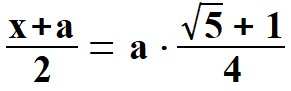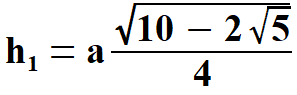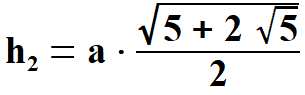Na podstawie wzorów na boki trójkątów z poprzednich obliczeń, można wyprowadzić przy okazji wartości funkcji trygonometrycznych dla kątów 36⁰ oraz dla 72⁰.
Na rysunku 2 widać kąty 36⁰ i dla 72⁰ w trójkątach, które już znamy. Przy wyprowadzeniu sinusów i kosinusów należy zawsze spojrzeć na trójkąty na rysunku 2, oraz w/w wzory.

RYS.1|RYS.2 + wzory

Otrzymujemy: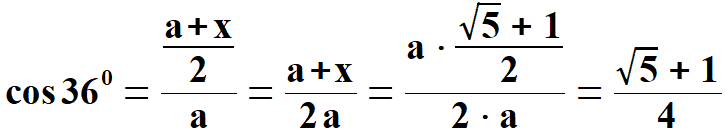

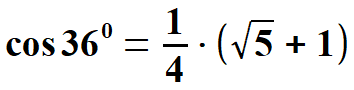
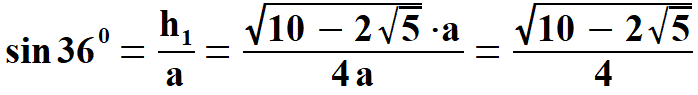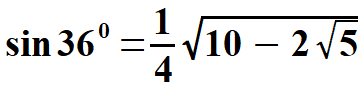RYS.1|RYS.2 + wzory

Obliczam dwie wielkości, które są potrzebne przy obliczeniu tangensa i kotangensa kąta 36⁰.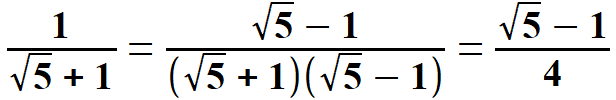

oraz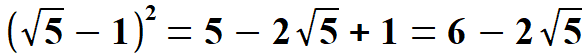

Obliczam tangens i kotangens.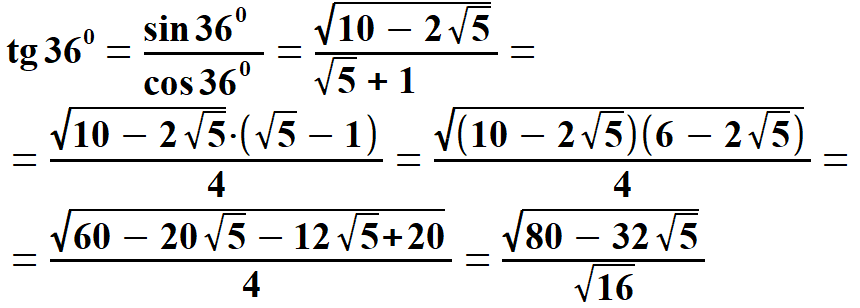

RYS.1|RYS.2 + wzory

Stąd po skróceniu otrzymujemy: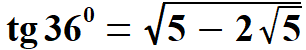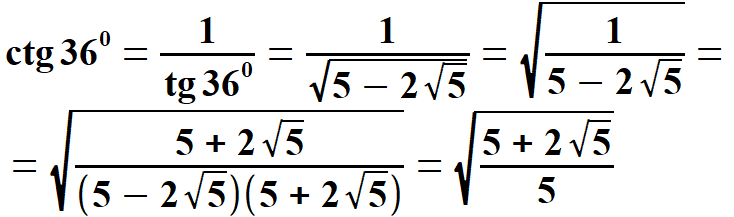

Po rozszerzeniu i wyłączeniu przed pierwiastek otrzymujemy: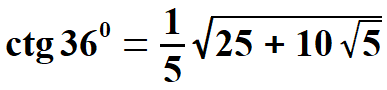

Na końcu przed wyprowadzeniem wzoru na pole pięciokąta foremnego pokażę wszystkie 8 wzorów na funkcje trygonometryczne w jednym miejscu.
Przechodzę do funkcji dla kąta 72⁰.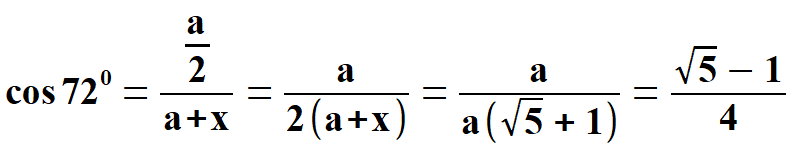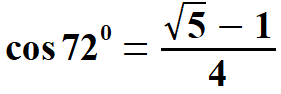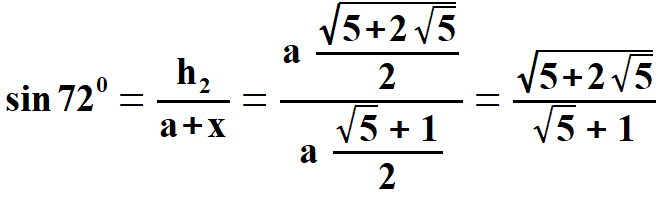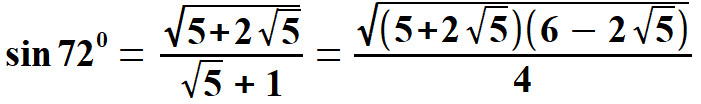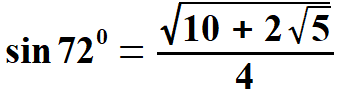

RYS.1|RYS.2 + wzory

Jak poprzednio wyliczę wielkość, która pomoże wyprowadzić wzory na tangens i kotangens kąta 72⁰.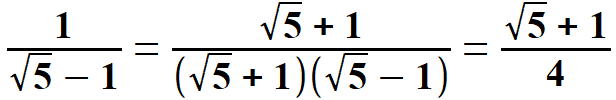

oraz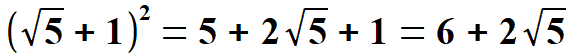

Wyprowadzam: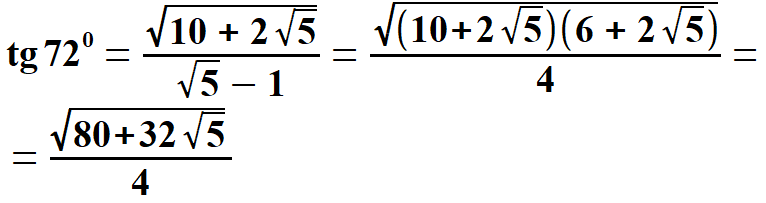

Po przekształceniu otrzymujemy: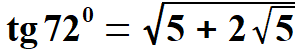

oraz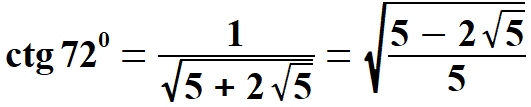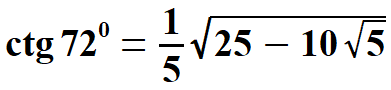

Zebrałem wyprowadzone funkcje trygonometryczne.

RYS.1|RYS.2 + wzory
a) dla kąta 36⁰

RYS.1|RYS.2 + wzory
b) dla kąta 72⁰

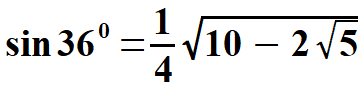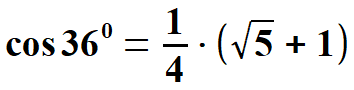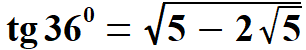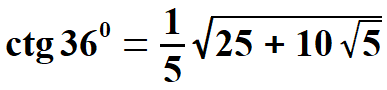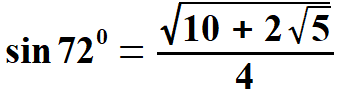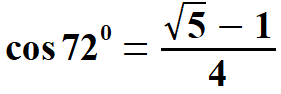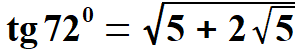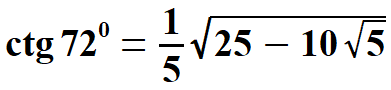Rys. 3

Obliczę teraz długość promienia R okręgu opisanego na pięciokącie foremnym. Długość tego promienia jest róna długościom ramion trójkątów równoramiennych, z których składa się pięciokąt ( rys. 3 ).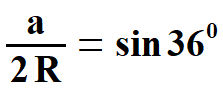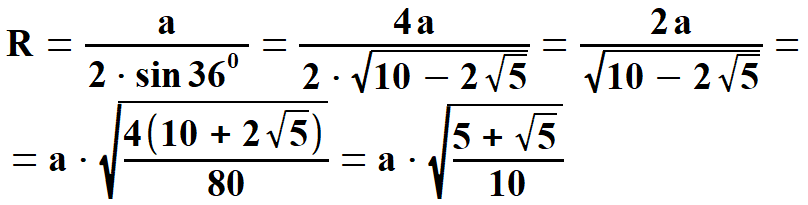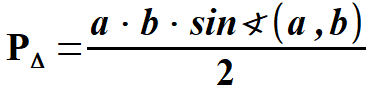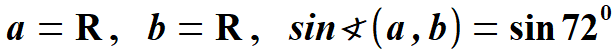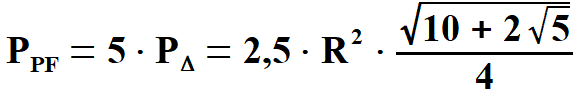

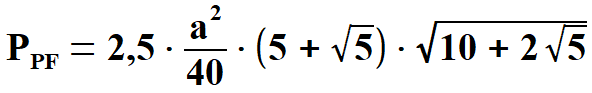Skorzystam ze wzoru obliczonego wyżej.

Obliczam pole jednego z trójkątów równoramiennych.

Powyższy wzór można przekształcić. Wchodzimy z nawiasem pod pierwiastek i otrzymujemy następujące przekształcenia.

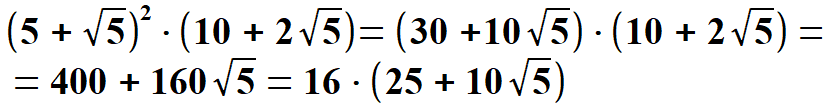
Po wyłaczeniu spod pierwiastka liczby 16 i dalszych przekształceniach otrzymujemy poniższy wzór.

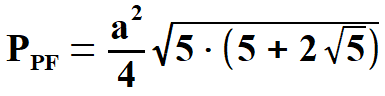Wzór na pole pięciokąta foremnego o boku a.
Wzór ten jest trochę inny niż wzór z poprzedniego wyprowadzenia. Poprawność obu wzorów zostały sprawdzone przeze mnie w programie geometrycznym Cyrkiel i Linijka.

UWAGA Dopiero kilka dni po zamieszceniu tych dwóch artykułów na stronie matematycznej znalazłem uzasadnienie równości obu wzorów.
Jak będę miał czas, pokażę to uzasadnienie.

POLE PIĘCIOKĄTA FOREMNEGO

Opracował: Mariusz Baszak

Pole pięciokąta foremnego trygonometria		MATEMATYKA W ZESPOLE SZKÓŁ W WIDUCHOWEJ			W matematyce nie ma drogi specjalnie dla królów	Powrót do głównej strony