Wiadomości o pierwiastkach dla klasy 8		MATEMATYKA W ZESPOLE SZKÓŁ W WIDUCHOWEJ			W matematyce nie ma drogi specjalnie dla królów	Powrót do głównej strony

POWRÓT DO WYBORU
DLA KLASY 8

PODSTAWOWE WIADOMOŚCI O PIERWIASTKACH

Przykłady pierwiastków.

Pierwiastek drugiego stopnia

2 - stopień pierwiastka, którego nie widać
5 - liczba podpierwiastkowa.

Dla pierwiastków drugiego stopnia nie piszemy liczby 2 oznaczającej stopień. Poniższe zapisy są równoważne:

Pierwiastek trzeciego stopnia

3 - stopień pierwiastka
7 - liczba podpierwiastkowa.

Pierwiastki drugiego stopnia nazywamy pierwiastkami kwadratowymi.

Pierwiastki trzeciego stopnia nazywamy pierwiastkami sześciennymi.

Uwaga: Pierwiastek drugiego stopnia z liczby a to taka liczba b, która podniesiona do potęgi drugiej jest równa liczbie a.

Jeżeli

Wiemy ile są równe wartości pierwiastków kwadratowych (drugiego stopnia) bardzo wielu liczb. Znamy je z potęg drugiego stopnia. Pokażę to na kilku przykładach.

ponieważ

Podobna sytuacja jest z pierwiastkami sześciennymi.

Uwaga: Pierwiastek trzeciego stopnia z liczby a to taka liczba b, która podniesiona do potęgi trzeciej jest równa a.

Jeżeli

Również znamy wartości z pierwiastków sześciennych (trzeciego stopnia) wielu liczb. Znamy je z potęg trzeciego stopnia. Ponieważ liczba ujemna podniesiona do trzeciej potęgi jest liczbą ujemną, istnieją pierwiastki sześcienne z liczb ujemnych. Pokażę to na kilku przykładach.

ponieważ

Łatwo również obliczyć pierwiastki drugiego i trzeciego stopnia z ułamków, których liczniki i mianowniki są odpowiednio drugimi potęgami lub odpowiednio trzecimi potęgami liczb naturalnych (o tych liczbach była mowa wyżej). Pokażę to na przykładach.

ponieważ

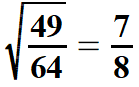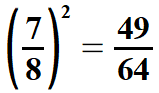
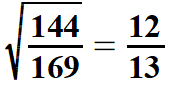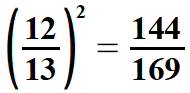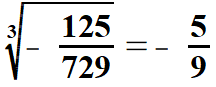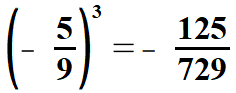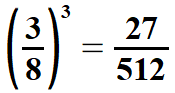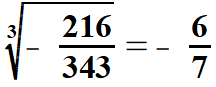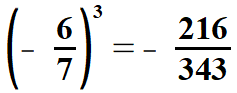Tak samo postępujemy pierwiastkując liczby mieszane. Jeżeli po zamianie liczby mieszanej na ułamek niewłaściwy, którego licznik i mianownik jest drugą potęgą liczby naturalnej to łatwo obliczyć z niej pierwiastek kwadratowy. Analogicznie jest z pierwiastkami sześciennymi liczb mieszanych. Pokażę to na przykładach, lecz już bez uzasadniania.

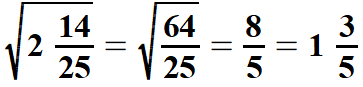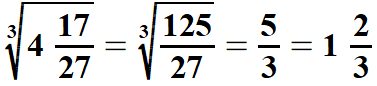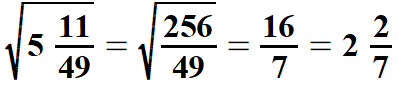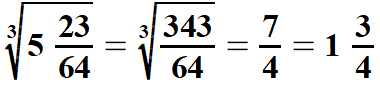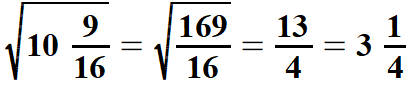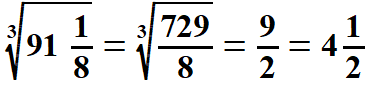Przykłady pierwiastków kwadratowych

Przykłady pierwiastków sześciennych

Pierwiastki kwadratowe ( drugiego stopnia), których wartości są równe od 2 do 20

Pierwiastki sześcienne ( trzeciego stopnia), których wartości są równe od 2 do 10

Podstawowe wzory dotyczące mnożenia i dzielenia pierwiastków.

Mnożenie pierwiastków o tych samych stopniach

mnożymy liczby podpierwiastkowe, a stopień zostaje bez zmian.

Wzory.

oraz

Dzielenie pierwiastków o tych samych stopniach

dzielimy liczby podpierwiastkowe, a stopień zostaje bez zmian.

Wzory.

oraz

powyższe wzory zapisujemy również w postaci ułamków

oraz

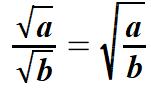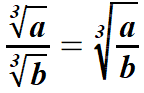Uwaga: Wzory dzielenia pierwiastków zostały już wykorzystane w obliczeniach pierwiastków z ułamków zwykłych. Można je też wykorzystać w pierwiastkowaniu ułamków dziesiętnych. Pokażę to na przykładzie.

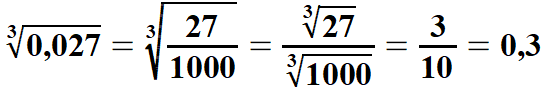z drugiej strony widać, że

stąd otrzymujemy

Wzory mnożenia pierwiastków są wykorzystywane do wyłączania liczby spod znaku pierwiastka. Należy liczbę podpierwiastkową rozłożyć na czynniki, tak aby otrzymać przynajmniej jeden czynnik, z którego można obliczyć pierwiastek. Pokażę to na przykładach.

Wzory mnożenia pierwiastków są wykorzystywane również do włączania liczby pod znak pierwiastka. Należy liczbę stojącą przed pierwiastkiem zamienić na pierwiastek z jej odpowiednio kwadratu dla pierwiastka kwadratowego lub pierwiastek z jej sześcianu dla pierwiastka sześciennego. Pokażę to na przykładach.

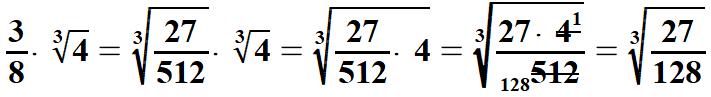Uwaga: W działaniach na pierwiastkach pod liczbami mogą kryć się różne potęgi, z których można obliczać pierwiastki.
Należy dobrze zapamiętać to co zostało pokazane na początku tej strony:

1) pierwiastki kwadratowe, których wartości są równe od 2 do 20,

2) pierwiastki sześcienne, których wartości są równe od 2 do 10.

Widać to w powyższych przykładach.