Wiadomości o potęgach dla klasy 8		MATEMATYKA W ZESPOLE SZKÓŁ W WIDUCHOWEJ			W matematyce nie ma drogi specjalnie dla królów	Powrót do głównej strony

POWRÓT DO WYBORU DLA KLASY 8

POWRÓT DO NACOBEZU POTĘGI I PIERWIASTKI

PODSTAWOWE WIADOMOŚCI O POTĘGACH

Przykłady potęg.

Potęga

2 - podstawa potęgi,    7 - wykładnik potęgi.

Potęga

3 - podstawa potęgi,    4 - wykładnik potęgi.

Przykłady obliczania potęg.

oraz

Uwaga: Dla potęgi liczby ujemnej otrzymujemy (-15 jest w nawiasie, więc do potęgi podnosimy liczbę -15 ):

Jeżeli jednak minus stoi przed całą potęgą to otrzymujemy (tylko podnosimy do potęgi liczbę 15, minus dopisujemy do potęgi):

Należy zwrócić uwagę na potęgi o wykładnikach 1 oraz 0.

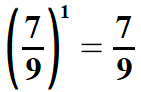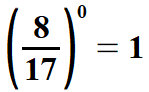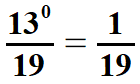
W ostatnim przykładzie jest podniesiony do potęgi tylko licznik, ponieważ ułamek nie jest wzięty w nawias.

Potęgi drugie nazywamy kwadratami liczb. Mają one wykładnik równy 2.

Kwadrat liczby 23 to , gdzie 23 jest podstawą potęgi,    2 jest wykładnikiem potęgi.

Potęgi trzecie nazywamy sześcianami liczb. Mają one wykładnik równy 3.

Sześcian liczby 17 to , gdzie 17 jest podstawą potęgi,    3 jest wykładnikiem potęgi.

Kwadraty (potęgi o wykładniku 2) liczb od 2 do 20.

Sześciany (potęgi o wykładniku 3) liczb od 2 do 10.

Potęgi liczby 2 o wykładnikach od 2 do 10.

Potęgi liczby 3 o wykładnikach od 2 do 5.

Podstawowe wzory dotyczące mnożenia potęg.

Mnożenie potęg o tych samych podstawach

dodajemy wykładniki, a podstawa zostaje bez zmian.

Wzór 1.

Przykłady

Dzielenie potęg o tych samych podstawach

odejmujemy  wykładniki, a podstawa zostaje bez zmian.

Wzór 2.

Wzór można zapisać w postaci ułamka.

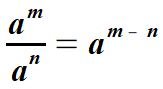Przykład

Mnożenie potęg o tych samych wykładnikach

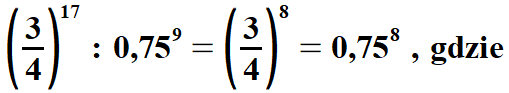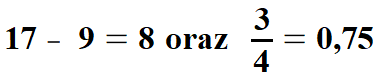mnożymy podstawy, a wykładnik zostaje bez zmian

Wzór 3.

Przykład

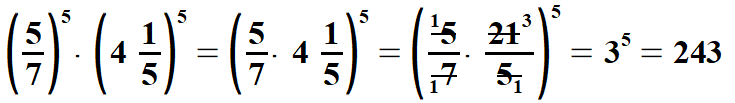Wzór powyższy możemy zapisać w postaci odwrotnej.

Przykład

Dzielenie potęg o tych samych wykładnikach

dzielimy podstawy, a wykładnik zostaje bez zmian.

Wzór 4.

Wzór można zapisać w postaci ułamka.

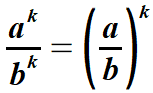Przykłady

W poniższym przykładzie wykorzystujemy powyższy wzór w obu postaciach. Uwaga: Liczba a oraz liczba b są ilorazami dwóch liczb. Należy dobrze przeanalizować ten przykład.

Potęgowanie potęgi

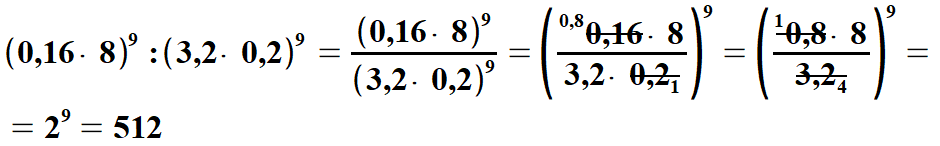mnożymy wykładniki, podstawa zostaje bez zmian.

Wzór 5.

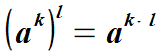Przykłady

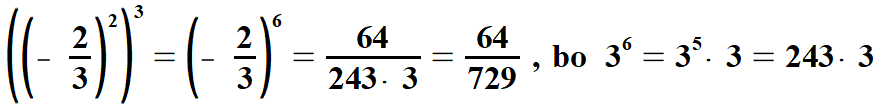W powyższym przykładzie liczba 6 jest wykładnikiem parzystym, stąd wartość potęgi jest dodatnia.

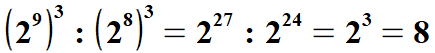Uwaga: W działaniach na potęgach pod liczbami mogą kryć się różne potęgi. Należy dobrze zapamiętać to co zostało pokazane na początku tej strony:

1) kwadraty liczb od 2 do 20,

2) sześciany liczb od 2 do 10,

3) potęgi liczby 2 o wykładnikach od 2 do 10,

4) potęgi liczby 3 o wykładnikach od 2 do 5.

Widać to w poniższym przykładzie.

Wiedząc, że oraz otrzymujemy:

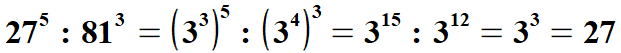Należy to wziąć pod uwagę przy rozwiązywaniu zadania domowego.